Statistical Modeling for Practical Pooled Testing During the COVID-19 Pandemic
Published in arXiv preprint (2021) - Under Review., 2021
Joint work with Saskia Comess, Hannah Wang, and Susan Holmes.
Pooled testing offers an efficient solution to the unprecedented testing demands of the COVID-19 pandemic, although with potentially lower sensitivity and increased costs to implementation in some settings. Assessments of this trade-off typically assume pooled specimens are independent and identically distributed. Yet, in the context of COVID-19, these assumptions are often violated: testing done on networks (housemates, spouses, co-workers) captures correlated individuals, while infection risk varies substantially across time, place and individuals. Neglecting dependencies and heterogeneity may bias established optimality grids and induce a sub-optimal implementation of the procedure. As a lesson learned from this pandemic, this paper highlights the necessity of integrating field sampling information with statistical modeling to efficiently optimize pooled testing.
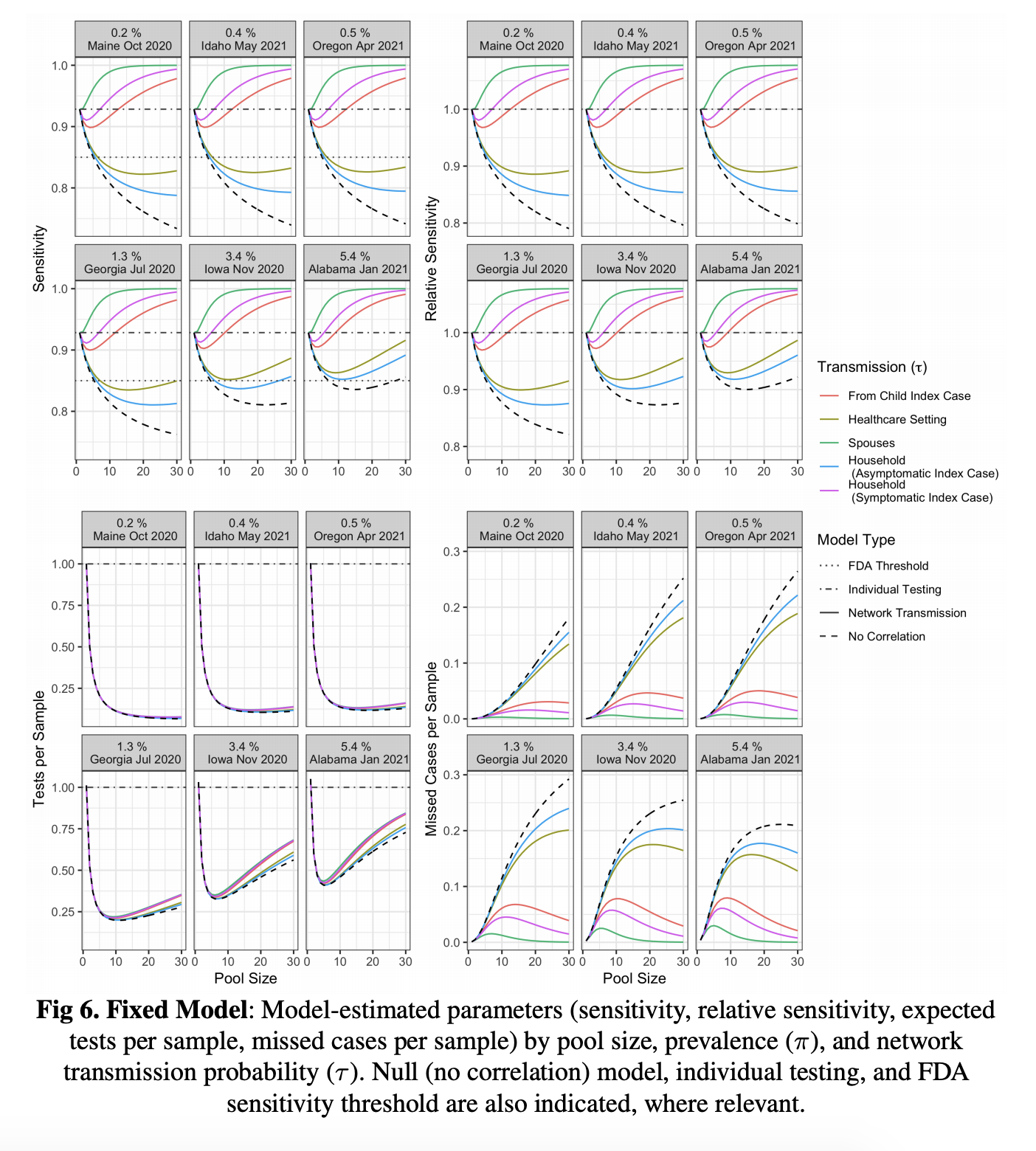
Using real data, we show that (a) greater gains can be achieved at low logistical cost by exploiting natural correlations (non-independence) between samples – allowing improvements in sensitivity and efficiency of up to 30% and 90% respectively; and (b) these gains are robust despite substantial heterogeneity across pools (non-identical). Our modeling results complement and extend the observations of Barak et al (2021) who report an empirical sensitivity well beyond expectations. Finally, we provide an interactive tool for selecting an optimal pool size using contextual information.
Recommended citation: Comess, Saskia, Hannah Wang, Susan Holmes, and Claire Donnat. “Statistical Modeling for Practical Pooled Testing During the COVID-19 Pandemic.” arXiv preprint arXiv:2107.05619 (2021). Under Review.
