Claire Donnat

Claire Donnat

Assistant Professor in Statistics

Posts by Collection

publications

Large-Scale Subspace Clustering for Computer Vision

Published in Signals, Systems and Computers, 2016 50th Asilomar Conference on, pp. 1014-1018. IEEE, 2016, 2016

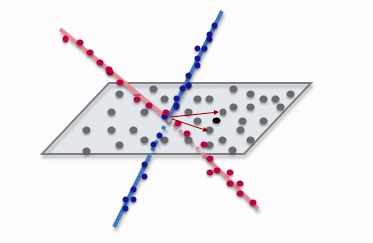
Subspace clustering is an unsupervised technique that models the data as a union of low-dimensional subspaces. Here, we propose a divide-and-conquer framework for large-scale subspace clustering, allowing it to scale up to datasets of more than 100,000 points.

Recommended citation: Chong You, Claire Donnat, Daniel P. Robinson, and René Vidal. "Large-Scale Subspace Clustering for Computer Vision." http://ieeexplore.ieee.org/abstract/document/7869521/

Tracking network distances: an overview

Published in Annals of Applied Statistics 12.2 (2018): 971-1012, 2018

In this work, we study distances between sets of aligned graphs. In particular, we try to provide ground and principles for choosing an appropriate distance over another, and highlight these properties on both a real-life neuroscience and microbiome applications, as well as synthetic examples.

Recommended citation: Donnat, Claire and Holmes, Susan (2018). "Tracking network distances: an overview." Annals of Applied Statistics 12.2 (2018): 971-1012.

Learning Structural Node Embeddings Via Diffusion Wavelets

Published in The 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, August 19-23, 2018, London, United Kingdom, 2018

We introduce GraphWave, a method for discovering structural similarities on graphs. In particular, GraphWave represents each node s network neighborhood via a low-dimensional embedding by leveraging heat wavelet diffusion patterns.

Introduction to Geometric Learning in Python with Geomstats

Published in Proceedings of the 19th Python in Science Conference, 2018

We introduce geomstats, a Python package for Riemannian modelization and optimization over manifolds. With operations implemented with different computing backends (numpy, tensorflow and keras), geomstats provides a unified framework for Riemannian geometry and facilitates its application in machine learning.

Download here

Convex Hierarchical Clustering for Graph-Structured Data

Published in IEEE Transactions on Signal Processing, 2019

We extend the robust hierarchical clustering approach to the analysis of Graph-Structured data. Having defined an appropriate convex objective, the crux of this adaptation lies in our ability to provide: (a) an efficient recovery of the regularization path - which we address through a proximal dual algorithm - and (b) an empirical demonstration of the use of our method.

Recommended citation: Donnat, Claire and Holmes, Susan. (2019). "Convex Hierarchical Clustering for Graph-Structured Data." IEEE Transactions on Signal Processing. http://donnate.github.io/files/main_HC.pdf

Constrained Bayesian ICA for Brain Connectomics

Published in arXiv (Under submission), 2019

We investigate a constrained Bayesian ICA approach for connectome subnetwork discovery. In comparison to current methods, simultaneously allows (a) the flexible integration of multiple sources of information (fMRI, DTI, anatomical, etc.), (b) an automatic and parameter-free selection of the appropriate sparsity level and number of connected submodules and (c) the provision of estimates on the uncertainty of the recovered interactions.

Download here

A Bayesian Hierarchical Network for Combining Heterogeneous Data Sources in Medical Diagnoses

Published in Proceedings of the Machine Learning for Health NeurIPS Workshop, 2020

The increasingly widespread use of affordable, yet often less reliable medical data and diagnostic tools poses a new challenge for the field of ComputerAided Diagnosis: how can we combine multiple sources of information with varying levels of precision and uncertainty to provide an informative diagnosis estimate with confidence bounds? Motivated by a concrete application in lateral flow antibody testing, we devise a Stochastic Expectation-Maximization algorithm that allows the principled integration of heterogeneous and potentially unreliable data types. Our Bayesian formalism is essential in (a) flexibly combining these heterogeneous data sources and their corresponding levels of uncertainty, (b) quantifying the degree of confidence associated with a given diagnostic, and (c) dealing with the missing values that typically plague medical data. We quantify the potential of this approach on simulated data, and showcase its practicality by deploying it on a real COVID19 immunity study.

Download here

Uncertainty Quantification in Networks with Applications to Brain Connectomics

Published in PhD diss., Stanford University, 2020

My PhD thesis focuses on providing some methodological tools for extending statistical inference and uncertainty quantification to graph-structured data — whether these graphs are observed or latent. Central to our thesis is the application of these tools to the analysis of fMRI data.

Download here

Modeling the Heterogeneity in COVID-19’s Reproductive Number and its Impact on Predictive Scenarios

Published in Journal of Applied Statistics, 2020

The correct evaluation of the reproductive number R for COVID-19 is central in the quantification of the potential scope of the pandemic and the selection of an appropriate course of action. In most models, R is modeled as a universal constant for the virus across outbreak clusters and individuals. Yet, due to the exponential nature of epidemics growth, this simplification can lead to inaccurate predictions and/or risk evaluation. In this perspective, instead of considering a single, fixed R, we model the reproductive number as a distribution sampled from a simple Bayesian hierarchical model.

Download here

talks

teaching

Teaching experience 1

Undergraduate course, University 1, Department, 2014

This is a description of a teaching experience. You can use markdown like any other post.

Teaching experience 2

Workshop, University 1, Department, 2015

This is a description of a teaching experience. You can use markdown like any other post.